Analytical Processes#

The aleatory.processes module provides classes for continuous-time stochastic processes which can be expressed in analytical form.

aleatory.processes.BrownianMotion
aleatory.processes.GBM
aleatory.processes.BESProcess
aleatory.processes.BESQProcess

class aleatory.processes.BrownianMotion(drift=0.0, scale=1.0, T=1.0, rng=None)[source]#

Brownian motion

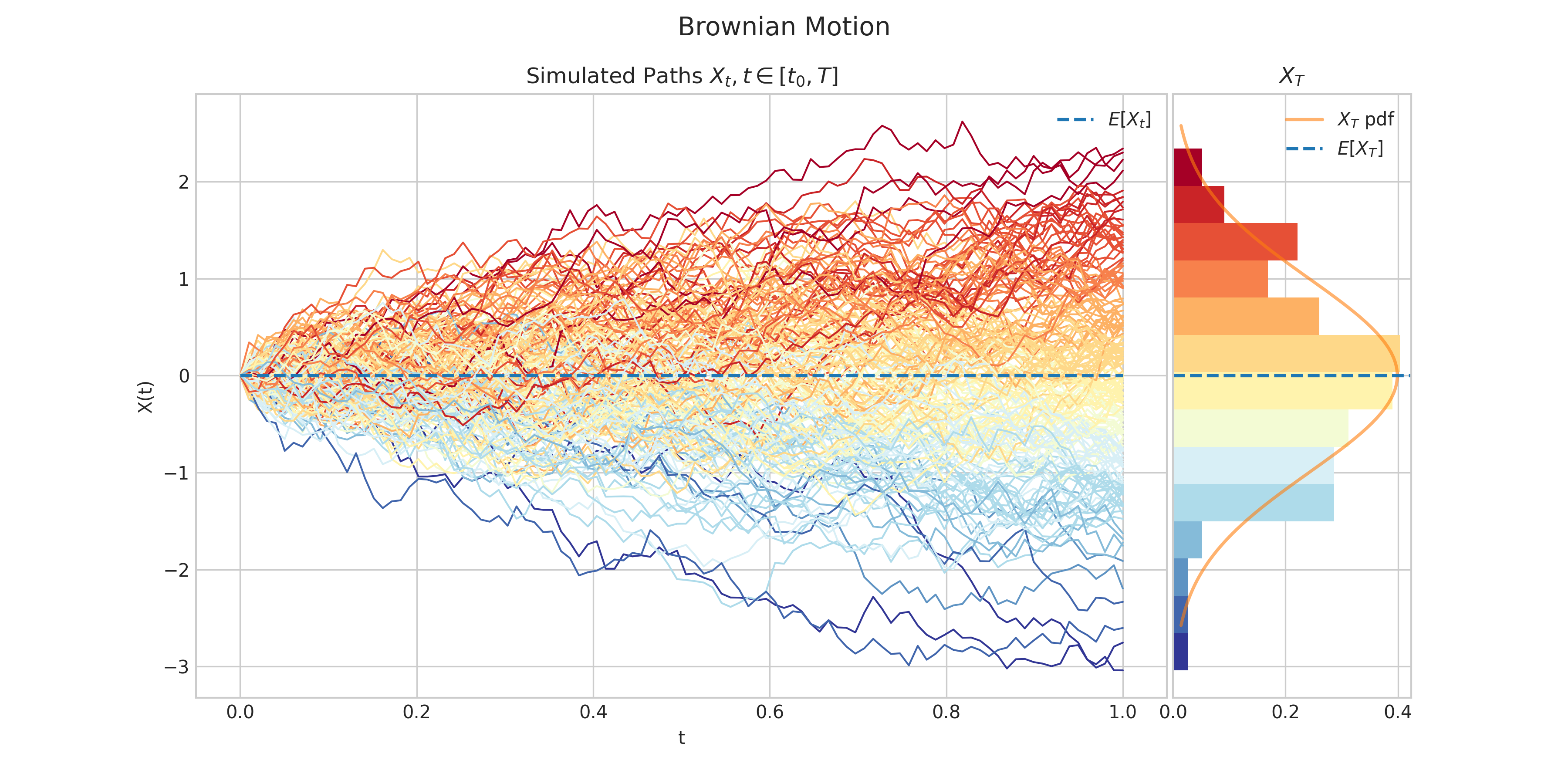
A standard Brownian motion \(\{W_t : t \geq 0\}\) is defined by the following properties:

Starts at zero, i.e. \(W(0) = 0\)
Independent increments
\(W(t) - W(s)\) follows a Gaussian distribution \(N(0, t-s)\)
Almost surely continuous

A more general version of a Brownian motion, is the Drifted Brownian Motion which is defined by the following SDE

\[dX_t = \mu dt + \sigma dW_t \ \ \ \ t\in (0,T]\]

with initial condition \(X_0 = x_0\in\mathbb{R}\), where

\(\mu\) is the drift
\(\sigma>0\) is the volatility
\(W_t\) is a standard Brownian Motion.

Clearly, the solution to this equation can be written as

\[X_t = x_0 + \mu t + \sigma W_t \ \ \ \ t \in [0,T]\]

and each \(X_t \sim N(\mu t, \sigma^2 t)\).

Parameters:

drift (float) – the parameter \(\mu\) in the above SDE
scale (float) – the parameter \(\sigma>0\) in the above SDE
initial (float) – the initial condition \(x_0\) in the above SDE
T (float) – the right hand endpoint of the time interval \([0,T]\) for the process
rng (numpy.random.Generator) – a custom random number generator

property T#: End time of the process.

draw(n, N, marginal=True, envelope=False, type='3sigma', title=None, **fig_kw)[source]#

Simulates and plots paths/trajectories from the instanced stochastic process.

Produces different kind of visualisation illustrating the following elements:

times versus process values as lines
the expectation of the process across time
histogram showing the empirical marginal distribution \(X_T\) (optional when marginal = True)
probability density function of the marginal distribution \(X_T\) (optional when marginal = True)
envelope of confidence intervals across time (optional when envelope = True)

Parameters:

n – number of steps in each path
N – number of paths to simulate
marginal – bool, default: True
envelope – bool, default: False
type – string, default: ‘3sigma’
title – string to customise plot title

Returns:

plot(n, N, title=None, **fig_kw)#

Simulates and plots paths/trajectories from the instanced stochastic process. Simple plot of times versus process values as lines and/or markers.

Parameters:

n – number of steps in each path
N – number of paths to simulate
title – string to customise plot title

Returns:

sample(n)[source]#

Generates a discrete time sample from a Brownian Motion instance.

Parameters:: n – the number of steps
Returns:: numpy array

sample_at(times)[source]#

Generates a sample from a Brownian motion at the specified times.

Parameters:: times – the times which define the sample
Returns:: numpy array

simulate(n, N)#

Simulate paths/trajectories from the instanced stochastic process.

Parameters:

n – number of steps in each path
N – number of paths to simulate

Returns:

list with N paths (each one is a numpy array of size n)

class aleatory.processes.GBM(drift=1.0, volatility=0.5, initial=1.0, T=1.0, rng=None)[source]#

Geometric Brownian Motion

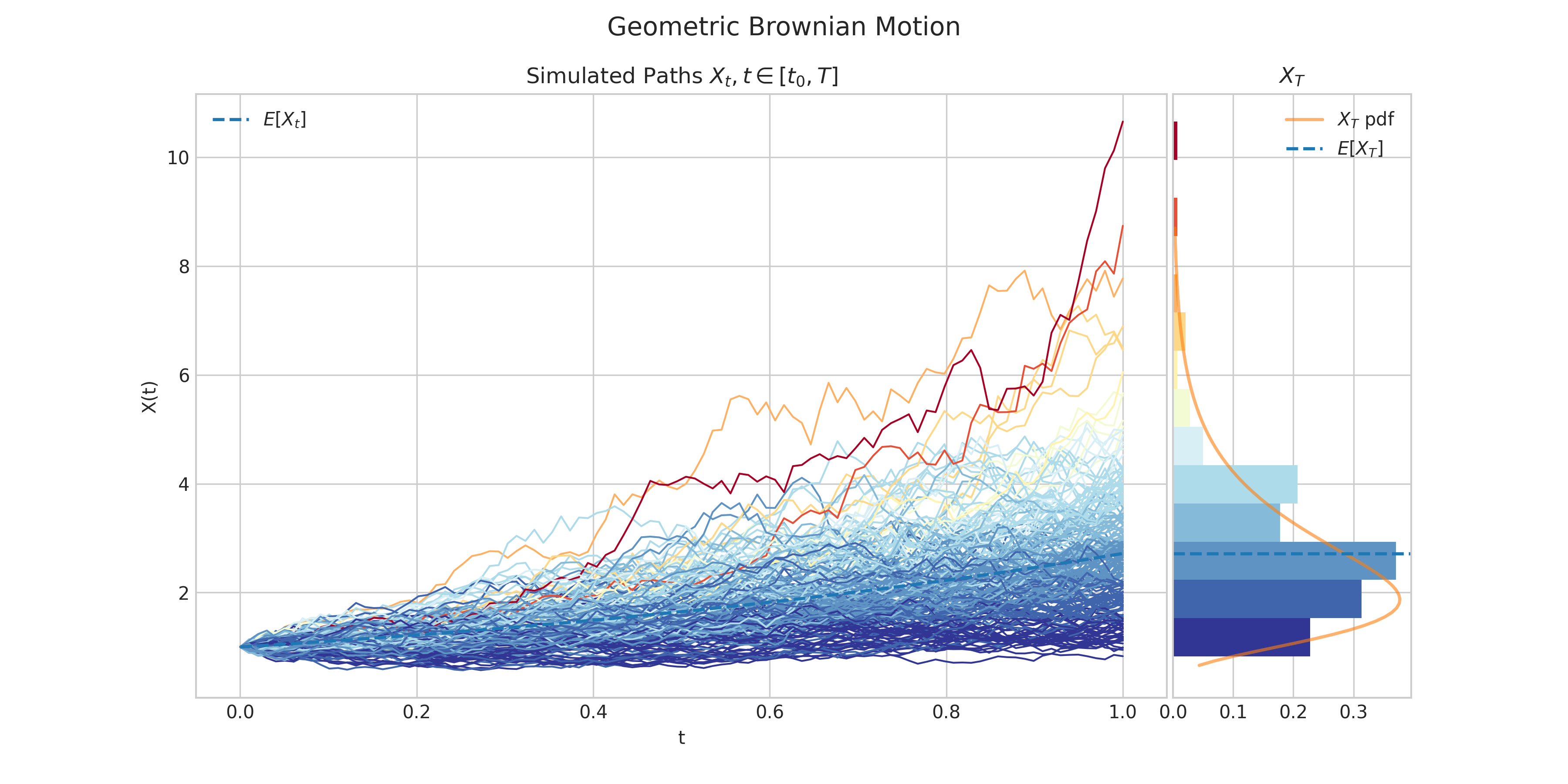
A Geometric Brownian Motion \(\{X(t) : t \geq 0\}\) is characterised by the following SDE.

\[dX_t = \mu X_t dt + \sigma X_t dW_t \ \ \ \ t\in (0,T]\]

with initial condition \(X_0 = x_0\geq0\), where

\(\mu\) is the drift
\(\sigma>0\) is the volatility
\(W_t\) is a standard Brownian Motion.

The solution to this equation can be written as

\[X_t = x_0\exp\left((\mu + \frac{\sigma^2}{2} )t +\sigma W_t\right)\]

and each \(X_t\) follows a log-normal distribution.

Parameters:

drift (float) – the parameter \(\mu\) in the above SDE
volatility (float) – the parameter \(\sigma>0\) in the above SDE
initial (float) – the initial condition \(x_0\) in the above SDE
T (float) – the right hand endpoint of the time interval \([0,T]\) for the process
rng (numpy.random.Generator) – a custom random number generator

property T#: End time of the process.

draw(n, N, marginal=True, envelope=False, title=None, **fig_kw)#

Simulates and plots paths/trajectories from the instanced stochastic process. Visualisation shows - times versus process values as lines - the expectation of the process across time - histogram showing the empirical marginal distribution \(X_T\) - probability density function of the marginal distribution \(X_T\) - envelope of confidence intervals

Parameters:

n – number of steps in each path
N – number of paths to simulate
marginal – bool, default: True
envelope – bool, default: False
title – string optional default to None

Returns:

plot(n, N, title=None, **fig_kw)#

Simulates and plots paths/trajectories from the instanced stochastic process. Simple plot of times versus process values as lines and/or markers.

Parameters:

n – number of steps in each path
N – number of paths to simulate
title – string to customise plot title

Returns:

sample(n)[source]#: Generate a realization.

sample_at(times)[source]#: Generate a realization using specified times.

simulate(n, N)#

Simulate paths/trajectories from the instanced stochastic process.

Parameters:

n – number of steps in each path
N – number of paths to simulate

Returns:

list with N paths (each one is a numpy array of size n)

class aleatory.processes.BESProcess(dim=1.0, initial=0.0, T=1.0, rng=None)[source]#

Bessel process

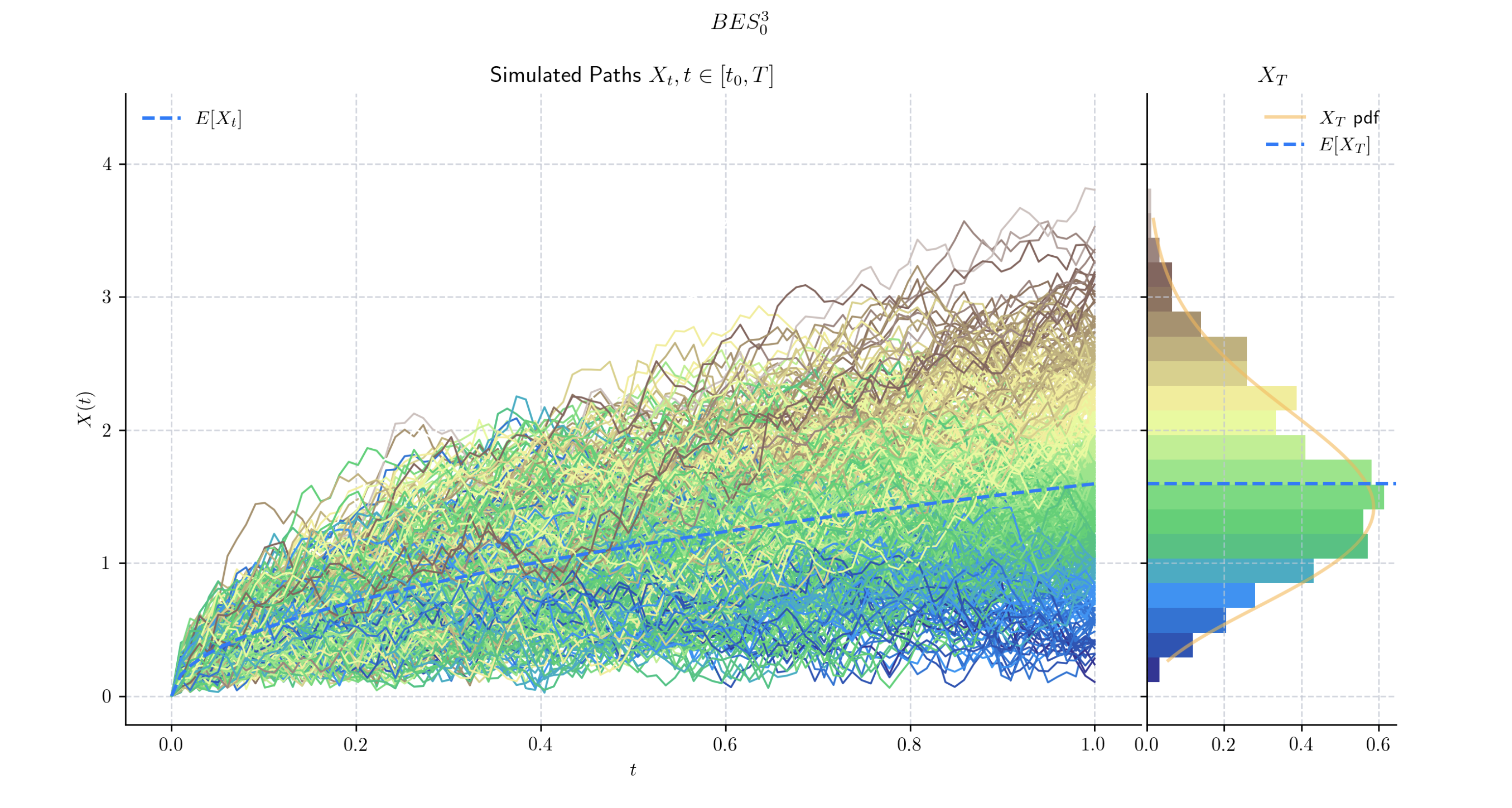
A Bessel process \(BES^{n}_{0},\) for \(n\geq 2\) integer is a continuous stochastic process \(\{X(t) : t \geq 0\}\) characterised as the Euclidian norm of an \(n\)-dimensional Brownian motion. That is,

\[X_t = \sqrt{\sum_{i=1}^n (W^i_t)^2}.\]

More generally, for any \(\delta >0\), and \(x_0 \geq 0\), a Bessel process of dimension \(\delta\) starting at \(x_0\), denoted by

\[BES_{{x_0}}^{{\delta}}\]

can be defined by the following SDE

\[dX_t = \frac{(\delta-1)}{2} \frac{dt}{X_t} + dW_t \ \ \ \ t\in (0,T]\]

with initial condition \(X_0 = x_0\geq 0.\), where

\(\delta\) is a positive real
\(W_t\) is a standard one-dimensional Brownian Motion.

Parameters:

dim (double) – the dimension of the process \(n\)
initial (double) – the initial point of the process \(x_0\)
T (double) – the right hand endpoint of the time interval \([0,T]\) for the process
rng (numpy.random.Generator) – a custom random number generator

property T#: End time of the process.

draw(n, N, marginal=True, envelope=False, title=None, **fig_kw)[source]#

Parameters:

n – number of steps in each path
N – number of paths to simulate
marginal – bool, default: True
envelope – bool, default: False
title – string optional default to None

Returns:

plot(n, N, title=None, **fig_kw)#

Simulates and plots paths/trajectories from the instanced stochastic process. Simple plot of times versus process values as lines and/or markers.

Parameters:

n – number of steps in each path
N – number of paths to simulate
title – string to customise plot title

Returns:

simulate(n, N)[source]#

Simulate paths/trajectories from the instanced stochastic process.

Parameters:

n – number of steps in each path
N – number of paths to simulate

Returns:

list with N paths (each one is a numpy array of size n)

class aleatory.processes.BESQProcess(dim=1.0, initial=0.0, T=1.0, rng=None)[source]#

Squared Bessel process

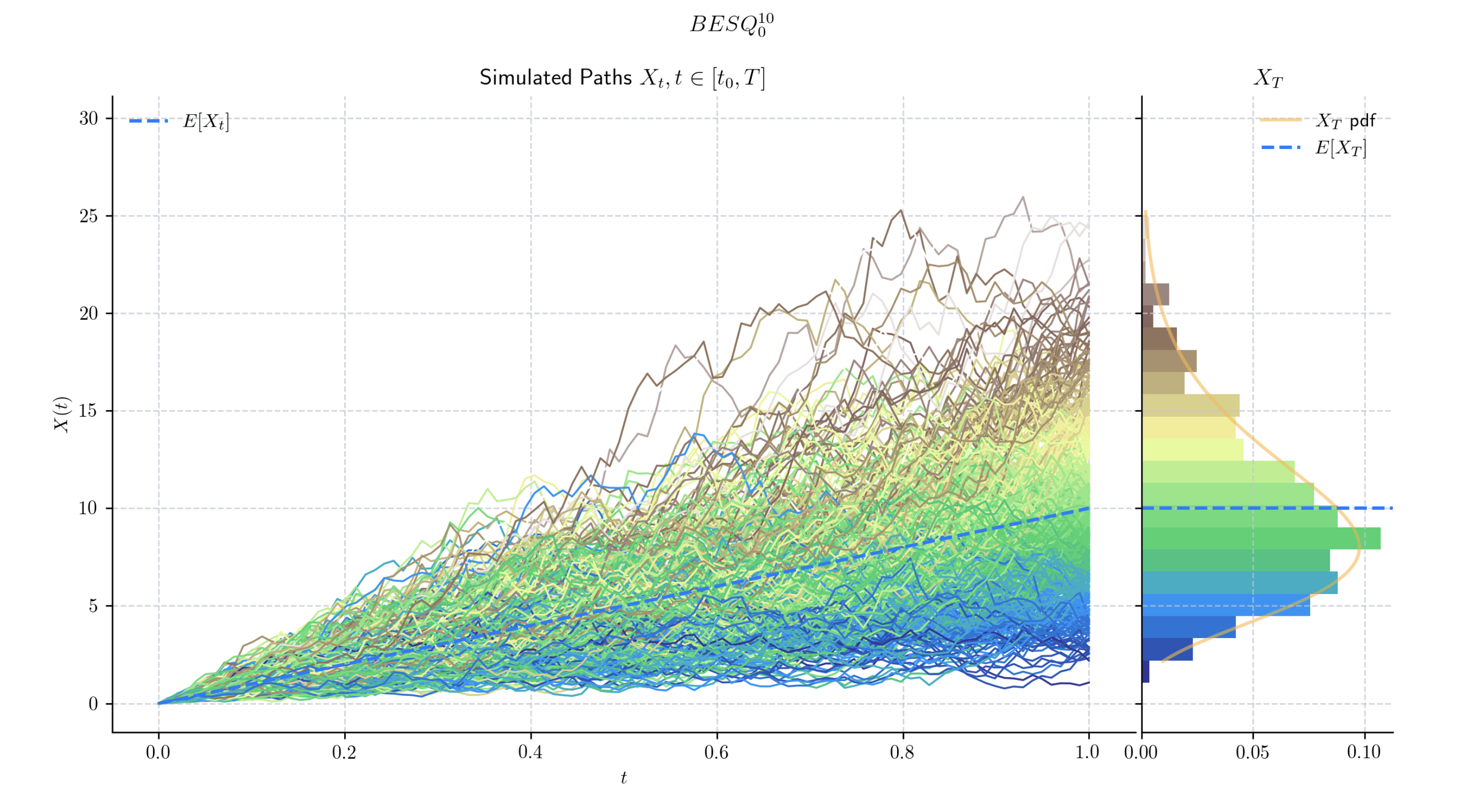
A squared Bessel process \(BESQ^{n}_{0}\), for \(n\) integer is a continuous stochastic process \(\{X(t) : t \geq 0\}\) which is characterised as the squared Euclidian norm of an \(n\)-dimensional Brownian motion. That is,

\[X_t = \sum_{i=1}^n (W^i_t)^2.\]

More generally, for any \(\delta >0\), and \(x_0 \geq 0\), a squared Bessel process of dimension \(\delta\) starting at \(x_0\), denoted by

\[BESQ_{{x_0}}^{{\delta}}\]

can be defined by the following SDE

\[dX_t = \delta dt + 2\sqrt{X_t} dW_t \ \ \ \ t\in (0,T]\]

with initial condition \(X_0 = x_0\), where

\(\delta\) is a positive real
\(W_t\) is a standard Brownian Motion.

Parameters:

dim (double) – the dimension of the process \(n\)
initial (double) – the initial point of the process \(x_0\)
T (double) – the right hand endpoint of the time interval \([0,T]\) for the process
rng (numpy.random.Generator) – a custom random number generator

property T#: End time of the process.

draw(n, N, marginal=True, envelope=False, title=None, **fig_kw)#

Parameters:

n – number of steps in each path
N – number of paths to simulate
marginal – bool, default: True
envelope – bool, default: False
title – string optional default to None

Returns:

plot(n, N, title=None, **fig_kw)#

Simulates and plots paths/trajectories from the instanced stochastic process. Simple plot of times versus process values as lines and/or markers.

Parameters:

n – number of steps in each path
N – number of paths to simulate
title – string to customise plot title

Returns:

simulate(n, N)[source]#

Simulate paths/trajectories from the instanced stochastic process.

Parameters:

n – number of steps in each path
N – number of paths to simulate

Returns:

list with N paths (each one is a numpy array of size n)